And finally, the monthly cycle [Part 1].

Not that monthly cycle.

I had a busy few weeks and I’m actually trying to build things instead of just write, so while I predicted I’d get to this post last month, I was off by a bit or so. That said, one of my most important posts I suppose, given my start in options trading and the NOPE, is simply understanding one of the most important calendrical effects in the market today - the monthly options expiration cycle.

One of the questions a new trader might have delving into options is why there are some tickers with very few expiries (also called tenors, in the context of time-to-expiry) and some with many. For example, the big kids on the block, SPY and its Nasdaq-sister QQQ, have multiple options expirations per week - more specifically, Monday, Wednesday, and Friday. On the other extreme, we see many smaller companies have only a monthly expiration. As a general rule of thumb, even in tickers with many expirations available, open interest (and hence traded options) tends to follow some pretty robust patterns:

• Options trading volume, for any given time, tends to be highest at the near-at-the-money strikes, with increasing drop-off as you get farther and farther away from the current spot price. This leads to an interesting anomaly - there tends to be, in markets, a cost associated with illiquidity (or conversely, a premium with liquidity). As options move deeper ITM/OTM and open interest and trading volume declines, spreads widen.

• With few exceptions, the general trend is that OI is highest in quarterly expiries, high in monthly, and scales downwards accordingly. While in anomalous instances weekly expiries can be highly traded (for example, during earnings or black swan events), in general the monthly expiry tends to be the most significant (quarterly, of course, falling on a monthly expiry).

Options close to expiry perform strangely. The more mathematical reason for this comes from the concept of an option - at expiry, the value of an option contract is well defined (it’s simply whatever the current spot price is minus the strike of the option). However, at any time before expiry, even an infinitesimally short time before expiry, the option has what we call “optionality” - there is some ambiguous chance it expires in the money (and hence has well defined value at expiry) and some other chance it expires out of the money.

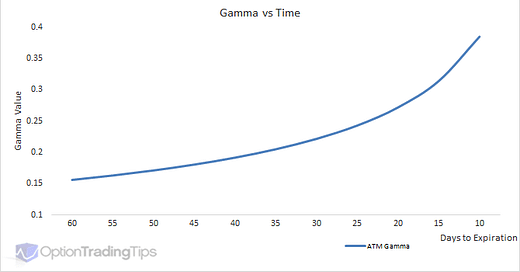
This is the fundamental reason for, as we described in the Intuitive Greeks series, gamma, or the rate at which option delta changes as underlying price does, increases as you get close to expiry. This is harder to visualize, but relates back to understanding Queen Delta as a measure not only of hedging but chance of an option expiring in the money. An at-the-money option in general tends to be 50 delta (although not always!), which roughly means that there’s a 50:50 chance at expiry that the option expires in-the-money. This idea is fundamentally related to the volatility of the underlying - in a more volatile stock, given equal amounts of time remaining, we expect more strikes to potentially end up in-the-money for a volatile stock than a quiet one.

However, volatility is at least traditionally measured as a function of time (although other interpretations use other measures). Therefore intuitively, assuming volatility is constant (lol), we expect there’s more chance for a stock to move in price with more time remaining. This is why given enough time, very out-of-the-money options have some delta, but lose delta over time. This similarly impacts their gamma too, since gamma is a derivative of the delta.

More interesting to us, though, is what happens to options near or at-the-money. Volatility works both ways — it can, with enough movement, take an option that is currently in-the-money out, and an out-of-the-money option in. This leads to interesting behavior at the border.

Let’s imagine a scenario where we have a call option with strike $50, the underlying stock is at $50, and the option is just about to expire. In fact, it’s so close to expiring, that we have time for exactly one more price move. There are two outcomes:

1) If the next transaction moves the stock price to $49.99, since we have a call, it is now out-of-the-money at expiry. Therefore, it has 0 delta, and is worthless. This is the same outcome if the next transaction does not move the price at all (so the stock price stays at $50.00).

2) If the next transaction moves the stock price to $50.01, since we have a call, it is now in-the-money at expiry. Therefore, it has 100 delta, and is worth 0.01 * 100.

This is an absolutely massive differential in delta — a penny move in our stock price is the difference between 0 and 100 delta at expiry! While this example is contrived, this is exactly the reason gamma behaves so strangely — as we get closer and closer to expiry, we have room for much smaller moves, which means that out-of-the-money and in-the-money options both change delta less (so their gamma decreases), and at-the-money gamma increases dramatically. This follows a moderately parabolic curve:

The Market Maker’s Curse

Most of us know market makers as those vile people who make our derivatives expire worthless, but they’re not all bad. In fact, as I can talk about in later posts, they’re essential in many ways in keeping the market efficient and reasonably liquid.

But that’s not what this post is about.

The interesting thing to note about options is that unlike underlying (stocks), options can be created ad hoc based on good old supply and demand. Ignoring legal or risk-related requirements to hedge, an option is simply a promissory from one party to another party to give that party the right, but not the obligation, to buy or sell some quantity of an asset at a certain date/time. In an illiquid market, there of course is substantial risk in not having the assets (in the case of a call) or not having the cash (in the case of a put) on assignment, but there is no requirement per se (you could also simply just default). This is different than a share, which at least theoretically has a fixed float (ignoring the conspiracy theories about naked shorting), which is fixed regardless of supply or demand technical factors (at least over short time periods).

When you buy or sell an option, in general, your counter-party will be a market maker. This is especially true in more liquid option chains, and in general they help keep the spreads (bid-ask) tighter than in cases where there is an absence of market makers.

Market makers, however, in the most basic sense just try to profit off the bid-ask spread. In a more complicated example I’ll talk about in my next article(s), it’s actually a combination of exchange liquidity rebates and a tradeoff of informed trader risk that really determine profit, but the spread can be seen as the max potential profit of the traditional market maker.

In the best of cases, every buy order is matched to a sell order, and the market maker makes essentially a risk free profit. In reality, this rarely happens. This is what we call inventory risk - a market maker holding inventory has a directional bias in the underlying asset, and makes/loses money just like the normal rabble does. This isn’t a great position to be in, but it’s the cost of doing business, and we’ll talk more about it later on.

More importantly, options market makers attempt, in the best of times, to be delta neutral - that is, to hedge out the delta of the net options positions on their book (the combined portfolio of all their options positions). Succinctly, the net delta of the options market maker’s portfolio is their inventory risk. This is fairly straight forward — if my net delta is +50, for example, I could hedge out my book’s directional risk by shorting 50 shares of the underlying. In practice, this is more complicated, and most options market makers will try to hedge out sensitivity to higher order greeks, at least to some degree, as well. Hedging out Greeks, however, doesn’t need to only happen with shares — one can hedge with other options, or even with other related assets.

Let’s keep it simple, though. One of the most interesting impacts to the market maker occurs due to the action of gamma. Delta is, while beautiful and important, a fairly boring Greek, with a simple way to hedge. Delta acts linearly — I know, if I am long a 50 delta call option, that I will make $100 in PnL if the underlying moves up $1, or lose $100 if it moves down $1. Gamma introduces non-linearity into this equation — due to gamma, my delta will also change as the price changes, so I might end up making $120 with a $1 move upwards.

To stay delta neutral, therefore, is not an easy or inert process.

Let’s pretend we have a 50 delta call option with 5 gamma. We can also write this as .50 delta and 0.05 gamma; it’s simply convention (and in this author’s opinion, cleaner) to express the fractions without decimals. What this means is that for a $1 change in the underlying, we expect our delta to change by 5 (our gamma). So for a call option, as the underlying moves up $1, we should now see our option have 55 delta. Conversely, if it moves down $1, our delta should decrease to 45 delta.

This is important to our market maker, who wants to stay ideally delta neutral. At 50 delta, we can simply hedge out our inventory risk by shorting 50 shares of the underlying. But now the price went up, and now the call has 55 delta! This means that even with our 50 shares short, our net delta exposure is still 5 delta. We now have inventory risk, which means we’re vulnerable to price changes!

So, to rectify this, we have to short 5 more shares to bring our book back to flat. Delta neutral again.

While this is very simplistic, what’s important is there are actually two different scenarios here at play. In the above example, I described a market maker who is long the 50 delta call. What this means is that as price is going up, assuming the trader wanted directional exposure, they’re making money! Moreover, in this scenario, as the market is going up, the market maker is shorting shares, which is causing (perhaps infinitesimally) the underlying price to go down.

This occurs because the market maker is long gamma — as the market rallies, they are counteracting the rally (shorting shares). Similarly, if the market instead were to decline and the 50 delta call becomes a 45 delta one, they would be buying back shorted shares (5 of them) as the market is falling. When the market maker is long gamma, they are continuously moving against the direction of the market movement, towards the initial condition (mean reversion, essentially).

The opposite and more violent scenario, however, occurs, when our market maker is short gamma. In vanilla options, long and short gamma essentially maps to which party is long or short the option contract. This differs from delta which, although it is impacted by trade side, is largely determined by the option type. This leads to the following permutations, which both have equivalent delta/gamma magnitude for our market maker:

1) Short put

Delta: +

Gamma: -

2) Long call

Delta: +

Gamma: +

Let’s look at the behavior of our desperately delta neutralizing market maker if instead of being long a 50 delta call position, they’re short a 50 delta put. To neutralize the put initially, she can similarly short 50 shares. However, as the underlying falls in price, the put gains delta, according to its gamma (we can say 5 again, similar to our prior example). So our short position position now, as the market is falling, goes from 50 to 55 delta, causing us to short 5 more shares to re-neutralize our exposure. As in the long call example, shorting shares causes the underlying price to move down. Conversely, as the market moves up $1, the put loses delta, becoming 45 delta. Therefore, our market maker must buy back shares, further increasing the underlying price.

If you’re tracking so far, from the perspective of market, there’s an incredibly salient difference between how our market maker is impacting market price dependent on whether they are short gamma (as in the case where they are short the put) or long gamma (as in the case where they are long the call):

1) When the market maker is short gamma, the hedging behavior needed to return to delta neutrality intensifies the movement of the market. In the short put example, the put gains delta as the market spot price drops, meaning the market maker is shorting more shares and intensifying the selloff.

2) When the market maker is long gamma, the hedging behavior needed to neutralize delta counteracts the movement of the market. In the long call example, as the call gains delta (when the underlying spot price rises), the market maker responds by shorting shares, putting downwards pressure on the market. This reduces the intensity of market movements, making the market more mean-reversionary.

This example, however, is just one market maker, one option. In reality, there are thousands of market makers operating across the market, often in the same or similar assets. In reality, there is no way to know the true exposure of market makers in aggregate. There are many reasons why, the most obvious being trade direction. Open interest, for example, tells you nothing about who holds what option — we have no idea if an option is held by a yolo’ing GME ape (in which case there is no hedging) or a dutiful market maker. We can safely assume nearly all US equity options have a market maker on one side of the trade, but we can’t easily tell which side.

All models are wrong, some are useful. In practice, most models make assumptions, the most common based on option type (e.g. put versus call). More complex models, like those hosted by SqueezeMetrics or Hau Volatility, use assumptions of how the implied volatility surface is impacted pre- and post- transaction, in order to model direction of open interest and understand true market maker Greek exposure. Are their models closer to reality? Unfortunately with the market, there is no certainty, especially on complex, dynamic phenomena.

We do know a few things, however. From the above examples on long versus short gamma regime, we can observe how the market writ large should act.

In the more macrostructural perspective, we speak of “market movement” as realized volatility. Therefore, we can make two inferences on how the market should behave, based on this latent variable (the market makers’ net gamma exposure):

1) In a regime where net, market makers are short gamma, we expect increased realized volatility. This is because the rehedging of options intensifies market movements, as explained above.

2) Conversely, when market makers are long gamma, we expect decreased realized volatility. This is also due to rehedging, and tends to lead to mean reversionary periods where the market oscillates around an equilibrium price (at least, in the absence of market moving information).

While gamma exposure is latent, and all models of it are by nature wrong, the good news is there really isn’t a linear relationship here. We can largely view gamma regimes as categorical:

• Short gamma regimes

• Slightly long gamma regimes

• Long gamma regimes

• Very long gamma regimes

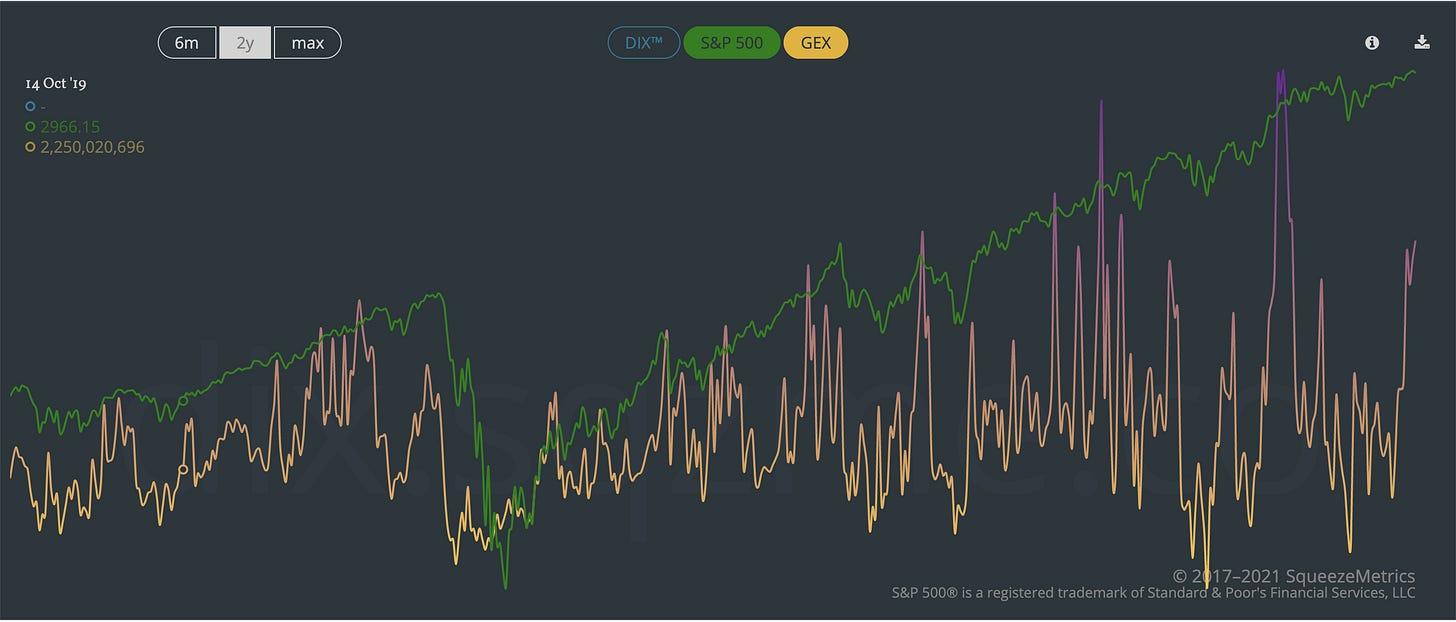
There is no fixed delineation here, and it does largely depend on assets. Meme stocks, for example, are in general in short gamma regimes, especially during the rally periods (this is because market participants rush to buy call options, meaning market makers are short a large amount of call options). The S&P however, is quite different. At least in recent years, the S&P (and for the most part other major indices) is in a long gamma state. We can observe through SqueezeMetrics’ GEX tool how this oscillates during the monthly period, which I will describe in more detail in the next part.

It’s very uncertain, however, if the forward relationship of realized volatility is “tradeable”. Despite common belief, with few exceptional periods hedging is not the dominant driver of index movement, and the predictability of realized volatility via gamma exposure is still heavily uncertain. Intuitively, gamma exposure and hedging matters more in the absence of market moving news, as well as when large institutional flows are minimal.

In the next post I’m going to talk a bit more about the structure of OI, vanna, and explain the rise of the MOPEX cycle in relation to popular buy-write and put-write strategies.

Cheerio,

Lily Francus