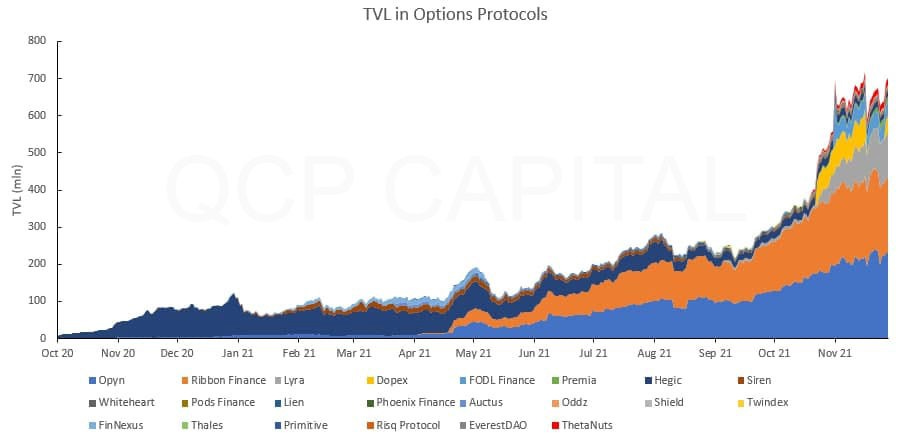
It’s kind of natural, when you think about it, that the original options-poster would have some thoughts on the potentially promising decentralized finance options markets, which seem to be having a moment:
While there exists some differences between vault implementations, the most common approach utilizes option-writing pools, which essentially write options by backing the contract by locking quote (in the case of put-writing) or base (for call-writing) assets for a set duration. In the case of Ribbon Finance, for instance, this writing occurs at preset intervals, with flow being auctioned (I believe in Ribbon’s case via Gnosis). In the case of Hegic, Premia, Dopex, and others, this occurs on a bespoke basis - options are written when a buyer interacts with the pool, meaning similar to traditional AMM architecture, yield is only created in a sustainable basis by actual demand for liquidity.
There are many interesting reasons to be optimistic on DeFi options. At its core, true decentralized options take advantage of smart contracts and settlement layers to avoid the need for centralized clearinghouses and exchanges which, turns out, can just reverse your nickel trades if they feel like it.
Perhaps more saliently, the DeFi options market tends to be richer in breadth than even CeFi alternatives like Deribit or CME, given that well, anyone can make a DeFi options protocol. So you can piss in the face of stuff like liquidity or worrying about options hedging notably impacting market movements.
We can do away with limiting nonsense like the need to own the underlying entirely as well. A derivative can become fully untethered from the idea of a reference underlying — much like the expansion of the CDS markets, in the absence of regulations and requirement for custody, there’s little except imagination preventing the options notional market size of a cryptocurrency or primitive from eclipsing the size of its underlying.
But the market, as is, grows under the sword of Damocles. This isn’t metaphorical - the structure of the market and preferred approach on a protocol basis is fundamentally unsustainable, and no amount of liquidity emissions can change that.
The issue is paying for risk.
Brief Options Review
Despite what many want to believe, Black-Scholes isn’t just some letters on a chalkboard. The pricing of derivatives is an interesting arcana mostly for retail traders, while more sensible people stick to delta-one trading so they don’t have to hedge their vomma exposure every full moon.
Black-Scholes, like most derivative pricing, is built on the idea of portfolio replication — given no actor preference, the price of a derivative should be equivalent to the cost of replicating a portfolio (uncreatively called the replicating portfolio) that, over the lifetime of the derivative contract, provides identical cash flows. Identical is doing heavy lifting in that sentence. In practice, very few contracts have a true perfect static (meaning, after t=0, no further buying or selling is needed to hedge during the contract’s lifetime) or even dynamic (further buying/selling/rebalancing) hedge. For example, during weekends and after-hours, vanilla equity options are largely untethered from implied price movements, given an option seller cannot easily rehedge their position while prices may change substantially. This creates gap risk and noticeable seasonality effects in equity volatility trading.
More on point — the cost of a vanilla option under Black-Scholes has a clear, non-mathematical interpretation. It is the expected cost, from the time an option is written to its expiry, of continuously re-hedging a portfolio consisting of the underlying in relation to its probability of ending up in-the-money (roughly its delta). It makes some clearly impractical assumptions, including of course:
Continuous hedging
Frictionless markets (so no transaction costs)
Log-normality of returns
We usually hand-wave these under the term basis risk, and have DLC packs added to the Black-Scholes model in order to try to match real-world pricing better.
Similarly, the Black-Scholes formula relies heavily on the notion of pricing implied volatility. Generally, this can be derived through back-solving the formula - starting with a decent seed guess (like historical volatility), we observe real-world prices and can compute a market price for implied volatility. This is an extremely dirty metric, since it not only accounts for true forecasted volatility over the lifetime of the contract, but also the added cost of basis risk.
But in practice, it tends to give us a good coordinate system for decomposing the very non-linear options payout (convexity) into a system of linear exposures (the Greeks). If we perfectly hedge a bought or sold option, we should expect to make zero profit, by the fundamental asset pricing theorem (akin to no-arbitrage). This is expected due to competition - as a market matures, powerful players (such as market makers) can warehouse risk much more efficiently (and often get niceties like maker rebates) than you can as a click-trading retail legend. This drives down the price to asymptotically return zero profit.
We can essentially simplify the payout of a continuously hedged vanilla option to be thus:
If forecasted volatility + cost of basis difference is greater than the actual realized volatility, the option buyer will make money.
If it is less than realized volatility, the option seller will make money.
If it is equal, neither party should make money.
In reality, there are several gotchas here. One well known divergence between theory and practice has to do with investor risk aversion - the price of puts is too damn high compared to their actual payout, especially on indices. But in matured markets scared by crashes like 1987, the price of protection can be high. This can be seen as a like-kind exchange - while the expected payout of puts for an index option writer tends to be positive over time, the left-tail risk of a crash of unknown severity is quite high. Something, something Taleb.
However, before I fly into an entirely new continent of tangents, the takeaway here is this — the price of an option in competitive markets isn’t an imaginary number, it is largely dictated by the anticipated cost to continuously rehedge the option (especially for European options).
Buy-Write isn’t Buying Right
When equity options markets weren’t speculative casinos serving the dark wishes of Citadel, there was believably a time where flow-insensitive selling of options at regular intervals made money. This is intuitive - the more illiquid the market, the less competition, but more importantly, the more desperate the buyers. In a truly illiquid market, you can assume most flow tends to be informed, and overcharge for the occasion.
However, owing to Robinhood and institutional demand for non-recourse leverage (and some other weird quirks, like rule changes post-2018 Volmageddon), the equity options market exploded. Competition also similarly exploded.
In the 2000s, many teams in the structured finance space noticed the “yield” potential of equity options, and came up with nifty-strategies very similar to what Ribbon Finance currently does:
Buy-write - This involves the purchase of stock and selling of covered calls against the stock. In the case the call ends up ITM, the stock is then repurchased shortly after to continue the strategy.
Put-write - This involves a large cash position and the selling of an equivalent nominal in put option contracts. If the put ends up ITM, the stock is acquired and sold to continue the strategy.
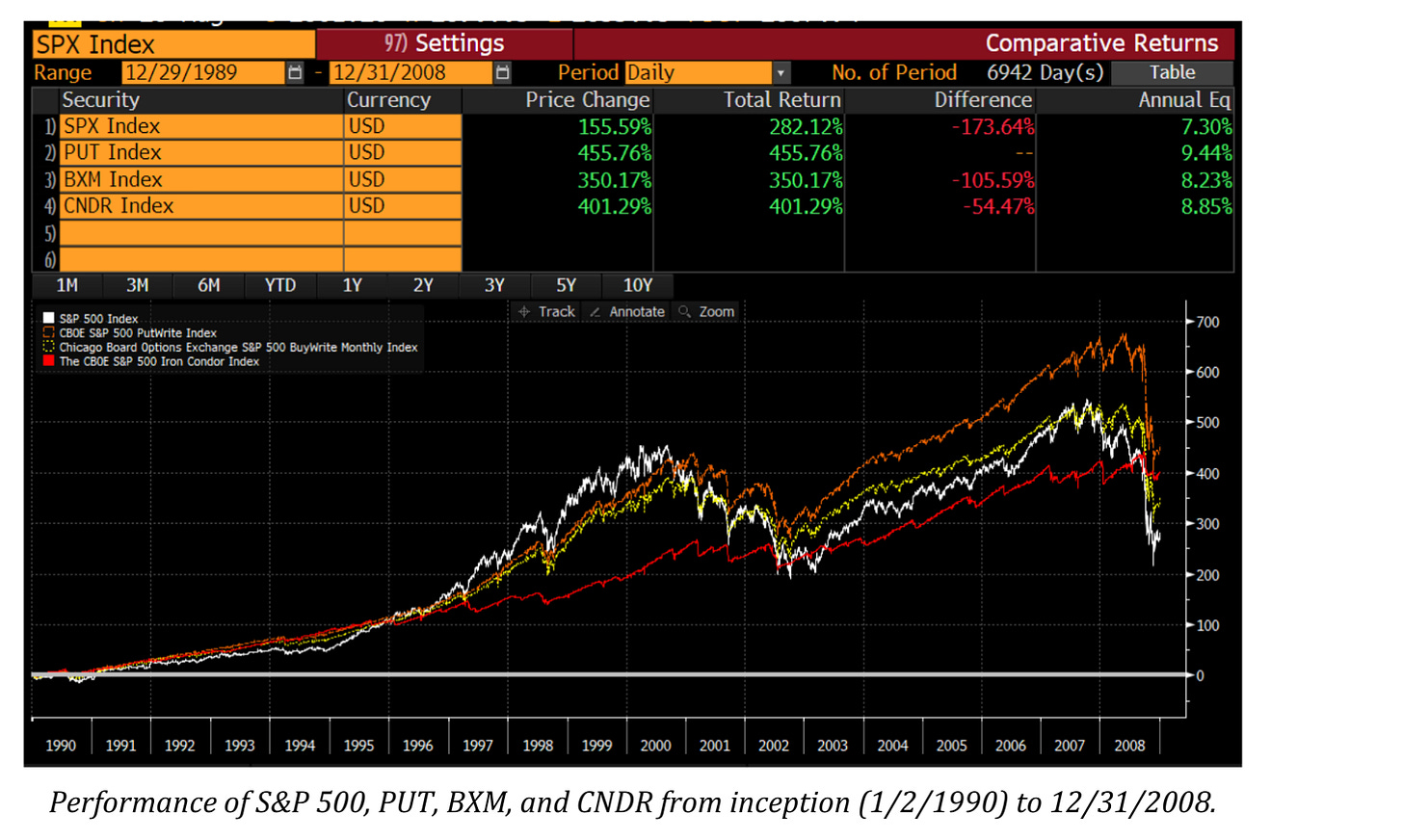
While there are certain modifications on both to try to be more clever, for a time they indeed were profitable. Pat Hennessy of IPS Strategic Capital has an excellent paper on this, “Is Selling Options Still Worth the Risk?”, with this beautiful backtest:
While it seems since 2018 luck has been squarely with the option buyers (we can observe that an SPX covered call struck 30-days out ATM lost money over the two year period), there was a time pre-2009 where the strategy of insensitive buy-write/put-writes was moderately profitable:
However, as the market matured, the premium for doing so dramatically compressed, and often flips negative.
This has a fairly intuitive basis - in a traditional buy-write (covered call) strategy, you are taking some variation of the Black-Scholes price (with some market IV), which is the fair price of risk assuming you can dynamically rehedge your position. In a statically-hedged buy-write strategy, you essentially hold 100 deltas worth of risk regardless of the option’s actual delta. While in some cases this will benefit you (you get exposure to market beta and drift in bull markets), in practice, you are capping your positive returns (due to the covered call) while leaving uncapped negative returns.
In the put-write case, we can argue this is primarily due to opportunity cost. While a put-write strategy, at least in equity options, will make money most of the time (negative skewness), it will lose a lot of money sometimes. But worse off, in truly outperforming periods (like November 2020 for SPX, for example, where it rallied 10% in a month), you do not see the equivalent upside. At best you will collect the put premium, which is priced in vol terms. While we assume volatility is largely symmetric, you assume uncapped downside risk (if the market mega-nukes) and capped upside risk (you cannot be paid out more than the put premium).
In short - neither a put-write nor a buy-write strategy will ever fairly compensate the writer for risk, since the market-competitive price for options (the premium) is based on the idea of dynamically hedging the option.
This is a problem for DeFi.
Fictitious money and capital efficiency.
From the above, it’s very clear what the fate of automated option sellers should be as the DeFi landscape matures. Right now, there are two obfuscating tailwinds which suggest even a naive buy-write/put-write might fare alright in the short term:
Liquidity incentives - Ignoring the idea of sustainable yield, many of these AMM-type protocols will provide regular emissions in a pseudo-equity token to liquidity providers to option pools, which based on speculative inflows, will often more than cover the anticipated loss from above. However, this is not sustainable — many of those pseudo-equities revolve around the idea of sharing future protocol yields. In the naive strategies above, the future expectation is that the protocols will never make money.
Market inefficiency - For most coins, a liquid options market does not exist. For many of these DeFi protocols, they also sell options in non-standard tenors and do not operate 2-sided market places, making it harder for informed flow to arbitrage price. It’s hard to really argue in the case of a LUNA option on a DeFi protocol, for example, what the fair price and IV should be if the volume is 5.
The problem, of course, is the latter benefits from the double-edged sword of illiquidity. While in the short term this obfuscates the brokenness of the system, in the long term, it will be impossible for an illiquid options market to compete with a liquid one. Similarly, at least from this author’s cursory look at Dopex and other DeFi protocols, DeFi options tend to run rich to CeFi (e.g. Deribit) alternatives. This makes sense from a liquidity provider perspective - I am inefficiently carrying risk, and the only way to staunch some loss is to price it rich. However, it also massively disincentivizes organic buying (not paid buying hoping for airdrops).
We can argue that the underlying cause of DeFi option underperformance at the limit will be capital inefficiency. For a clever buy-write liquidity provider (e.g. I provide ETH to let’s say Ribbon Finance which writes calls against it), I could run a local BSM model, and short perpetual swaps against my position, adjusting continuously to account for delta exposure. So it’s not necessarily I have to take on unnecessary spot risk (I even collect funding in most cases from that). However, in both the buy-write and put-write strategies, no matter what I do, I use significantly more capital than I would need to under a dynamic hedging regime. At the minimum, this is a real mark-to-market loss, given I could otherwise invest that capital for the contract’s duration at the risk-free rate.
There is no model given capital inefficiency that will correctly subsidize my expected loss here from simply overcollateralizing the position. In reality, one of the benefits for both the buyer and seller of an option is the synthetic leverage it affords and associated capital efficiency. Corey Hoffstein in his recent paper “Return Stacking” leans into this concept - leverage, well managed, is good. In the case of non-recourse leverage, you essentially can cut off the left tail and achieve higher returns.
The solution here for DeFi options is complicated. This author is decidedly bearish on the concept as it is current. There are brilliant teams working in the space with the best of intentions, but fundamentally the math will not work out in the traditional AMM model. This is a bit different in new primitives like Squeeth from Opyn Finance — in this case, Squeeth acts more like a total return swap based on the reference formula, which allows off-chain hedging and more capital efficient allocation.
Regardless, there is no free lunch between the former and latter. In an overcollateralized paradigm (the option vault) there is essentially zero counterparty risk on the derivative contract (the seller as a smart contract has all required collateral, and can only really default in case of a hack or breach). In the latter, there is substantial risk in truly illiquid markets. The mechanism usually hand-waved here is liquidation - a short Squeeth position, for example, can be liquidated. However, for the long side of that swap, what happens? In traditional marketplaces/clearinghouses, liquidity is sufficient enough due to dedicated market makers that a forcibly closed (buy-to-close) option position due to margin constraints can be rematched by another seller, removing counterparty risk. In thinly traded DeFi markets with no real centralized clearinghouse, this isn’t the case.
In a true liquidation cascade/crunch, we should anticipate some sort of forced closure of long positions in these DeFi swap markets. This is partly due to strong likelihood of correlated positioning by market participants (i.e. everyone will get nuked at once on the long side, rather than expecting sophisticated hedging strategies), and partly due to lack of dedicated market makers.
In the general case, most of these total return swap-like instruments operate abstractly as:
There is a contract between parties A and B, arbitrated by a smart contract. This takes the form of two tokens - a short token, which represents a notional amount of X with collateral $Y behind it, and a long token which represents a notional amount of X_1 with collateral $Y_1 behind it. At regular time intervals, the contract uses some method (an oracle usually) to update the cost to each party, taking $Z from A (B) to give to B (A). When the collateral backing the short or long token falls near some threshold, the party is liquidated.
This is implicitly a short volatility position for the protocol, as all types of liquidation risk are. To give an example from Alkimiya:
This method, while attractive from a capital efficiency perspective, has two drawbacks:
Liquidation risk is short volatility — for Alkimiya’s Silica contract, which represents mining yields, we anticipate relatively muted daily volatility which should be reasonably covered with the above collateral requirements. Moreover, mining yields are linear risks — we do not have convex exposure to some sort of risk factor (gamma for spot price for ex.).
“Inverted American option” structure - Personally, I’m sure there’s an actual name for this is traditional finance, but it escapes me currently. In Alkimiya’s model, the buyer is paying a set premium upfront with no method of early exercise (it’s a swap, so there is no equivalent to exercise per se). In exchange, the seller can decide to early exercise — by letting their account get liquidated.
This inverse American option is a moderately unique structure. In a liquid market, this may be identical to a classic European option - with dedicated market makers, a liquidated seller could be replaced with a more willing counterparty for the buyer. In practice, this is what occurs in centralized finance, where exchange-traded options are cleared by a centralized clearinghouse, like the Options Clearing Corporation. While in the most extreme cases this system can break down, in practice the counterparty of an option isn’t the individual selling it (and we generally treat the OCC itself as having zero counterparty risk).
While a static buffer (the 5% above) handles linear risks well, it may not in practice be sufficient for convex instruments. While it unlocks significant capital efficiency (essentially providing the synthetic leverage we all know and love) and hence should lead to more liquid markets, a static buffer will not work properly with options. We would expect in an identical structure with vanilla DeFi options (a static buffer) that the likelihood of breaking the contract would go to 1 in many common scenarios, at the expense of the buyer (and hence cause liquidity to dry up - no one would buy it).
However, the nice thing is that we have well known tools from derivatives arcana to price such a structure. While it isn’t identical to a European option, it largely reduces in the limits of liquidity and penalty sizing. With a large enough penalty (where the penalty is for example the total potential notional exposure of the option), the pricing becomes identical to our put-write/buy-write strategies. With enough liquidity, the penalty can tend toward zero, as the protocol can match every buyer to a new seller in case of liquidation.
At any given point in time, the calculus for the seller is simple - if I expect it is more profitable for me to break the contract (and pay the penalty), I will. This is not identical to the option going ITM, because of path dependency and margin efficiency. A fully ITM European option (100 delta) is more or less identical to a forward at the same tenor, which is available at most centralized exchanges for pretty high margin efficiency.
I’m not going to go into the pricing of this structure, because:
I don’t exactly know, and it is almost certainly not closed-form (it likely can be modeled as a binomial tree, similar to an American option, although I may be wrong:
It’s outside the scope of a Sunday morning article (plus Substack doesn’t support LaTeX I think).
Realistically, we would expect that such a structure would trade naively at some discount to a non-callable liability (the traditional European option available on Deribit). However, this largely depends on buyer risk of contract breakage. As the market becomes more liquid, or if the protocol can act (or hire) a reinsuring entity to absorb seller defaults in liquidity crunches, we would expect more and more parity between CeFi and DeFi equivalents. This reinsurer can be funded by the delta between seller discounted price (to the BSM model) and the market price (which, assuming full assurance from the reinsurer, can be priced at BSM + basis). However, the caveat is correlation of market positioning of sellers — in times of stress, we would anticipate full on liquidity crunches, and large blows to the reinsurance pool.
That said, this is probably the best solution in my view for DeFi options until true cross-margining becomes available. Without this sort of penalty-swap system, even though it behaves tacitly different than European options, you cannot get paid properly for your risks. Protocols can incentivize liquidity as they wish, but money cannot be printed indefinitely. Speculation ceases, and protocols will die.
This will, finally, allow DeFi to pay you properly for your risks.
Lily






Due to recent events, I deleted my X app. Looking for a substitute for fintwit
Please keep posting!