Risk frees and currencies: Part Three

A method of calculating risk premia.

In the prior posts, I argued that under a simple argument using a change of numeraire, we can back out a true risk-free rate in crypto, at least for proof-of-staking based currencies. This essentially relies on creating a temporary “currency-denominated risk-free rate” variable, which relaxes the idea of risk-free rates in general. Instead of zeroing all risk, we define the currency-denominated risk-free rate (CD RFR for short) as an investment possible only in a given currency that provides no additional risk versus simply holding that currency.

This allows us a neat mathematical trick, similar to the idea of carry trading in Part 1 — if we stake a currency and account for slashing risk (which can be diversified across all validators), we can shift nearly all risk to the exchange rate between our invested currency (let’s say ATOM) and our PnL currency (let’s say USD). This has a fairly intuitive basis — in a proof-of-stake model, the network’s security relies on staked assets as a mechanism to validate transactions and avoid the problem of “double-spend”. To caveat — I am not a blockchain engineer, although I have a computer science background. If you’d like to learn more about the specifics of blockchain and consensus algorithms, I’d suggest Tim Roughgarden (a professor at Columbia University)’s course, free on YouTube:

However, we can conventionally assume that the value of a cryptocurrency, like any other asset, reflects some discount related to probability of default and expected loss given default. Default, in the cryptocurrency sense, we can say is the likelihood that the network allows double-spend to occur; that is, the consensus algorithm used by the network fails to properly validate transactions. In the most naive case, we can assume all agreement failures are catastrophic; that, if a network permits a double-spend, the expected loss for a tokenholder is 100%. In practice, this is likely not true (but can be relaxed later on).

That said, while we’ve defined a neat trick to back out a CD RFR, it doesn’t really put food on the table. Whether we call it risk-free in ATOM or not, at the end of the day, any trade we put on will have to convert back to USD, and all we’ve done so far is shift variables around. The actual incurred risk is the same.

Thankfully, the markets are good, and give us a way to neutralize exchange risk as well. We call these forward agreements — in crypto-land, perpetual swaps (or perps) and futures.

---

Dynamically Hedging Risk

The creation of the perpetual swap agreement is probably one of the least-contested innovations truly belonging to crypto, solving the problem of liquidity fragmentation — in a standard futures market, the exchange provides different tenors for the same instrument, in homage to the primary real-world use case of futures markets (hedging for commodity usage). In practice, this also provides us a method to create a term structure, which tends to provide useful information on market expectations.

However, in fairly illiquid markets, it’s a problem. Different tenors are represented at the exchange and pricing level as different markets, and hence liquidity (open interest) gets fragmented across tenors. This can be catastrophic in extremely illiquid markets (altcoins, for example), since the lack of liquidity is reinforcing — no one wants to use a dead marketplace!

Perpetual swaps (and their new cousin, everlasting options) aim to solve this fragmentation by doing away with the idea of tenors, and simply providing a swap agreement to exchange cash flows. This represents a synthetic obligation in reference to the underlying — instead of buying “spot” ATOM, for example, we can take a position in ATOM-PERP, which tracks ATOM. This tracking is enforced by the concept of funding rates — the delta between the spot price and perp price (subject to some calculation) is paid out at regular intervals, incentivizing close alignment of prices.

In practice, this innovation has substantial ramifications for liquidity and crypto market structure. As a synthetic, the perpetuals market for an instrument can be much more liquid or even notionally larger than the spot market cap, simply because it doesn’t necessarily have to be hedged with spot (although it usually is). More interestingly for us, the perpetuals market unlocks the idea of positive borrow rates - in conventional equities, for example, the short position relies on location of underlying shares, where the short seller will pay some floating borrow rate to the true owner for the privilege of shorting. In the swap context, given no spot has to be located, this requirement goes away; often (usually, in fact), the short party of the swap will be paid the funding rate.

This, similar to our previous example of the futures basis trade, creates the idea of a perpetual basis trade, where one can market neutrally long the spot (or future) and short the perpetual, collecting the funding rate. While the funding rate is usually positive, much like the futures basis, it can go negative at times (which we will discuss later). In those scenarios, the arbitrageur can promptly close out the trade at a profit (given the perpetual will now trade below the underlying), or take a loss waiting for the funding rate to revert.

The existence of the perpetuals and futures markets are important to backing out an RFR from our CD RFR. Much like the carry trader in Part 1, we can construct the following trade:

1. At time 0, we purchase spot currency A and short the perpetual A-PERP on exchange Q, both in notional size (in A) Z_0. We can define the exchange rate AUSD_t to represent the exchange rate between A and USD for all time t.

   • Notably, we should observe that the notional size in USD terms between the perpetual short and the spot purchase is different, due to the premium/discount of the perp. This tends to be marginal, but in practice you’d need to ensure both have equal sizing in A terms to neutralize exchange risk completely.

2. At time 1, we stake A in such a way that we diversify slashing risk.

   • In practice, full diversification is nearly impossible, due to minimum staking sizes and user experience. However, protocols like Lido allow the existence of validator pools and trusted validators, which do reduce staking risk (at the expense of risk of Lido Protocol, of course).

3. We define staking as a floating payout C_t * Z_{t-1} paid out in A units for all time t, where C_t is the staking yield for 1 unit of A at time t, and Z_{t-1} is the notional size in A units of our staked position. For every payout we have two options:

   • Reinvest payout - Given our payout, we can choose to add it to our long staked position Z_{t-1}, for a total of Z_t + C_t * {Z_t-1} units staked right before time t+1. This can either be neutralized (by shorting similarly C_t * Z_{t-1} units of the perpetual/futures, but similarly requires margin/collateral) or not (however this incurs currency risk).

   • Sell immediately - Assuming the market is liquid, we can immediately sell the staked proceeds for USD, incurring minimal currency risk (there is some small gap in time between recognition of staking payout and sale in which our exchange rate may change). This payout will be Z_{t-1} * C_t * AUSD_t in USD terms (although in practice we have transaction fees).

4. We can define the funding rate timestep t*, where at every positive real multiple of t* we incur some funding amount f_t * Z_t, which is a real number. This is paid out immediately on all notional size only at the funding time, not on a pro-rata basis; if we liquidate our position at 1.5t*, for example, we have incurred funding at t* but not at 2t*.

While certain blockchains payout in non-unit currencies (e.g. LUNA will pay out in a mix of LUNA and stablecoins for staking) in practice we can use dynamic hedging of our short perpetuals/futures position in order to hedge out currency risk. For #3 reinvestment strategy, we can define the following recursive relationship for the notional size of our staked position:

Z_{t+1} = C_t * Z_{t-1} + Z_{t}

We can assume the following:

1. It can be between -Z_{t-1} and positive infinity — we can never lose more when staking than our entire principal, but are relatively unbounded in our gains in A terms (in practice, likely much less than +Z_{t-1}.

2. Z_{t} = Z_{t-1}, t > 0 — Essentially, we just assume past our initial deposit, there will be no further investment from us other than potential reinvestment of staking dividends.

Sell Immediately

If we choose to sell immediately, the math is fundamentally simple, given the size of both of our short and long positions is never greater than the above formula (for each timestep, we sell all proceeds and make Z_{t-1} * C_t * AUSD_t. Given that at the end of each timestep, we sell any staking dividends, our position size will always be equal post-sale to Z_0. Similarly, we have hedged our constant size Z_0 for the lifetime of our trade, meaning we incur no exchange risk on it (at the end of our trade, net transaction fees, we should expect to have made $0 on currency fluctuations on Z_0).

Critically, however, we should notice that we incur slashing risk throughout the duration of this trade. With some non-zero probability for all time periods, we incur the risk of loss on our staked assets in proportion to the slashing penalty innate to the network. Slashing, though, is a network-specific design and can also involve no true loss of principal; instead, it may involve timeouts on yields (which can be modelled retrospectively as a loss on the next period’s earnings, for example). For mathematical simplicity, we can assume that the slashing penalty is effectively 0 for now.

Given this, our total PnL for the trade is largely from cumulative staking yields, the change in exchange rates, and the funding rate we pay, we can express it as follows:

P(t) = sum_\{i=1 to t}(Z_0 * C_i * AUSD_i - transaction fee) + sum_\{i=1 to floor(t, t*)}(Z_0 * f_{i * t*}) + transaction fees to hedge Z_0

Or in simple English — the profitability of selling staked proceeds immediately (in USD) is equal to the proceeds from selling it plus the cost (or profit) of hedging it via the perpetual. More simply, we can also hedge it via shorting the associated future, which provides a fixed funding cost/premium — the basis.

Reinvest Payout

Conversion to a closed-form approximation may be challenging, and largely depends on the shape of the instantaneous staking yields distribution, which differs on a currency-specific basis. This is because fundamentally we can’t make simplifying assumptions of the recursive relationship, since at each time period, our staking yields fundamentally depend on the prior time period’s payout. This similarly impacts our funding cost as well.

Empirically, we can start by observing if true staking yields can be fit to an existing distribution, again in A currency terms (the author has not done this yet).

The Exchange Risk Premium

As we noted, the ability to instantaneously sell proceeds from staking coupled with the ability to delta hedge the principal to exchange rate fluctuations gives us nearly a risk-free rate mechanism.

The keyword here is nearly.

In practice, this is still a dirty risk-free rate. Why? Because at the end of the day, who is letting us hedge our principal?

We can, in the most extreme example, argue that we have moved our spot long currency to stake it off-exchange or protocol into the most secure wallet known to crypto-kind. We can argue a near-instantaneous delta between staking payout and sale back into USD (although arguably we bear risk here, due to the cost of fiat on/off-ramping). However, at the end of the day, we must be constructing our hedge (the perpetual or future) through some sort of protocol or exchange, which in the worst case, can steal all or part of the money. Or most famously, in times of crashes, hacks, or extreme price fluctuations, you may simply be unable to close the trade at all. Simply put - your hedge itself is a risk.

Notably, in the case where the spot long is staked off-exchange while the perpetual remains on-exchange, you have asymmetric risk conditioned on price direction:

1. If the price of spot declines from the start of the trade, you have risk of losing your collateral backing the perpetual, as well as any unrealized gains on the short future (which cancels out your spot losses).

2. If the price of spot increases from the start of the trade, you have risk of collateral loss, but overall make money (since you no longer have unrealized loss on the short future).

However, we can realistically assume that exchange risk is probably correlated to crypto price direction (which tends to hold true across crypto-assets, given high price change correlation at the current time) — likely, a true exchange loss will occur unfavorably from a risk perspective (it will be when the price of spot declines).

We can define two terms — an implied exchange risk premium and a realized exchange risk premium. This holds to traditional definitions - an implied risk premium is the market’s expectation (over the next time period for example) while the realized is the actual risk (which can simply be the probability of exchange risk event * expectation of loss given event).

With little loss of generality, we can make a few assumptions here on the exchange risk premium:

1. For a given exchange, the implied exchange risk premium may fluctuate over time, but should be constant over all non-freely-convertible markets on the exchange for that time (given crypto has no cost of carry). We could make an argument that more liquid assets would be preferentially stolen (as well as more private ones) however.

   1. In freely convertible instruments between exchanges or off-chain (e.g. spot markets), we should not see a risk premium occur due to no-arbitrage. However, futures and perpetuals are not freely convertible, for example.

2. The implied exchange risk premium likely negatively correlates to crypto market capitalization and volumes and positively correlates to realized volatility. An exchange with higher volumes and usage is more likely to be safe and make consistent transaction fees — hence more likely not to steal your money. Conversely, if crypto is crashing, it may at a given point make economic sense for an exchange or exchange-affiliated actor to steal all your money.

3. The implied risk premium can be modeled as the cumulative probability of an exchange risk event * the loss given the event occurs. This implies farther tenors should hold proportionally higher risk premium than nearer tenors, given the only guaranteed approach to collect the basis is to hold to convergence at maturity.

4. In an efficient market, the expectation of the difference between implied and realized risk premium should be 0, in the absence of investor preference (aka risk aversion, similar to VRP in options).

We can observe the exchange risk premium in the one-currency, one-exchange model (we can call it (A, Q) for short - the previously explained trade model).

Subject to liquidity risk, whether I choose to hedge the staked spot with a perpetual swap or a futures instrument, I can similarly close out the trade at any point. In the futures basis trade, I have a fixed premium or discount over the lifetime of the trade, with a guarantee ex exchange risk of price convergence on the future’s maturity date. Conversely, the perpetual provides a floating funding rate, determined at every given time period, based on the difference between perp and spot prices.

Naively, in the absence of real-world factors like cross-margining, transaction fees, convenience yield, and capital constraints, we should expect that the futures bases across exchanges should be similar, save for the implied exchange risk premium. This would be a premium at the rate of the collateralization needed for the futures position rather than the notional, since that alone represents anticipated loss from the exchange risk event.

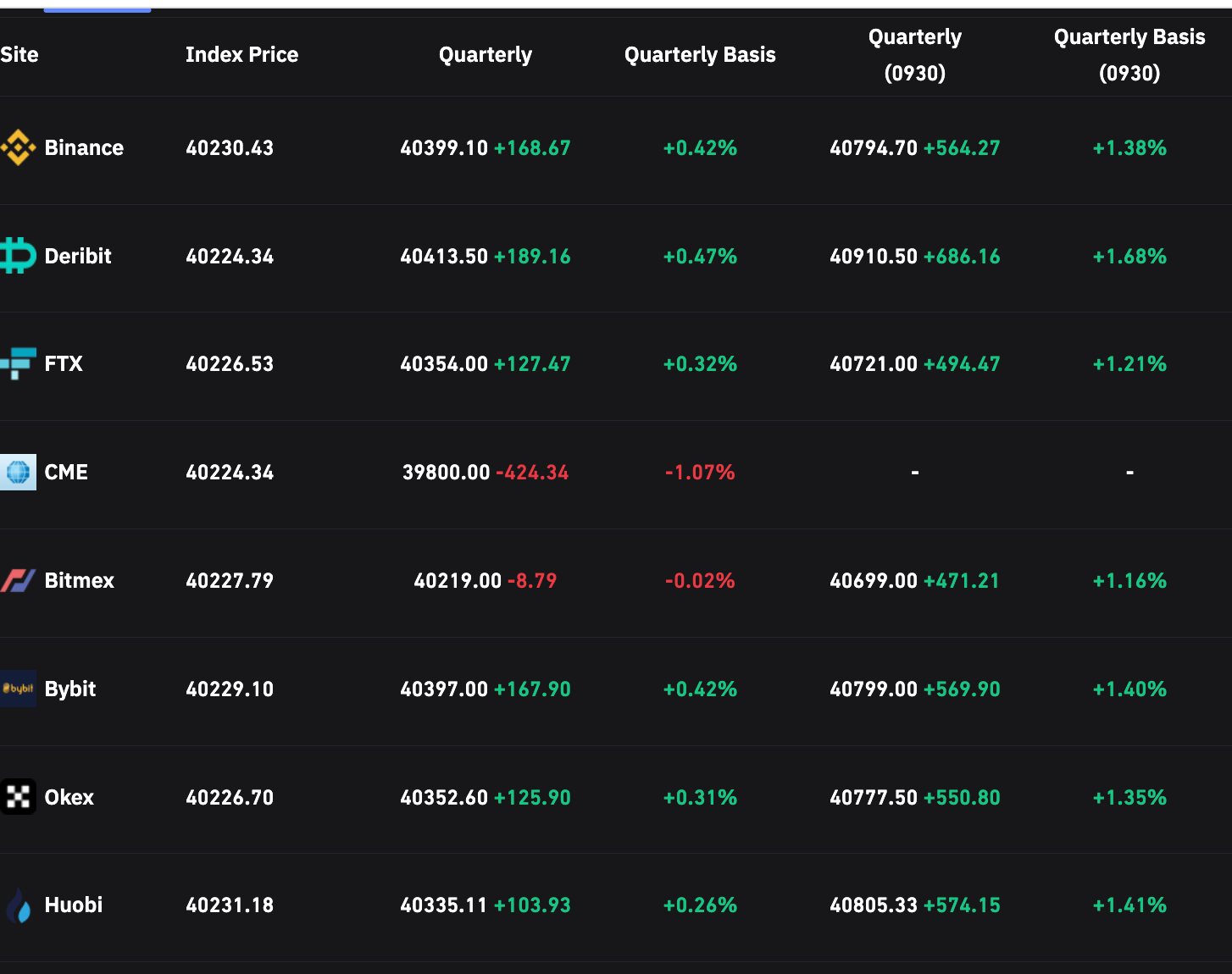
This provides us an interesting set of linear equations. If we look at the Bitcoin futures basis, for example, we can see the basis is largely aligned across exchanges currently:

Source: https://www.coinglass.com/Basis

However, this represents an instantaneous view, rather than one that holds across time. As anticipated theoretically, we’d assume that the implied exchange risk premium magnitude positively correlates to time-to-maturity, given the only guaranteed method of premium collection is to hold to convergence (maturity).

For all observed exchanges, in an efficient market, we can fit a risk premium model by using our first assumption - that the exchange risk premium for a given exchange is identical across all markets on the exchange for a given time t.

Likely, however, this model still isn’t perfect. As noted by many — especially in the case of perpetuals — there is an implied demand for leverage which does impact exchange and market-specific bases. I expect that as the market matures and frictions between exchanges decline (and more money flows into capturing the crypto basis trade market) that the demand for leverage impact on basis pricing will decline dramatically.

The Three Parities of Crypto

A clever reader will note already that there’s several explicit relationships that should exist in an efficient market based on what we’ve discussed so far:

• There is an instantaneous relationship between expected staking yield and funding rates - In the absence of demand for leverage and other yield sources, the funding rate represents the expected market-neutral return for staking a currency, minus a risk-free rate. This is partially distorted by the difficulty of on- and off-ramping capital into crypto, and reflects various “dirty” premia (aforementioned exchange risk and demand for leverage).

  • Notably, the staking yield relationship here does not need to account for inflation. Funding rates and exchange short positions already account for the “inflation” tax - for a fixed notional size of A, in the absence of inflows, AUSD_t will decline over time according to the inflation rate differential.

• There is an instantaneous relationship between expected currency move and funding rates - This was actually noted first by David Holt on Twitter, in which he essentially rediscovered uncovered interest rate parity in crypto. This is implied between expected staking yield and funding rates — staking yield, for all conventional matters, is the interest rate differential. This holds better or worse at times, and is sensitive to inflows and other factors (yield sinks like Anchor Protocol).

  David Holt @IDrawCharts

  Merry Christmas, here's some genuine free alpha that you can use Funding Rate vs Realized Drift automation not required most of y'all think of the funding rate like RSI; negative = oversold, positive = overbought but you're wrong, it's way more specific

• There is an implicit relationship between cumulative expected staking yields and futures bases ex. exchange risk - As we discussed, one can construct via #2 “Sell Immediately” a delta neutral trade via staking the spot currency and shorting the future. This is necessarily “dirty” - if we sell immediately, our PnL on the trade is determined in large part by the changes in exchange rates over the lifetime of the trade. However, it is still always positive profit - you will never sell the staked payouts an incur a net loss on the trade. However, principally by no-arbitrage, we should expect a strong intrinsic relationship between staking yields and futures bases due to the existence of this otherwise-arbitrage.

• There is an implicit relationship between cumulative funding rates and futures bases. - By the same rules above, we should expect that the futures bases and the cumulative funding rate over the same time period on the same exchange show implicit parity. Any deviations can be arbitraged out, ex exchange risk premium.

These relationships, in this author’s view, represent the true sources of sustainable yield generation in the crypto ecosystem. Expected staking yield, in this paradigm, represents the continued demand for blockspace, with staking yield (ex. the current inflation rewards model, a form of liquidity bootstrapping) intrinsically tied to demand for transaction confirmation and network utilization.

More interestingly, we can see a beautiful symmetry here.

Funding rates and staking yield both represent floating rates, while futures bases similarly represents a fixed rate over a given time period. In the funding rate and staking yield abstract example, we should not be further compensated for exchange risk significantly, due to the short duration (exchange risk becomes noticeable as a cumulative risk premium). However, it becomes important in understanding the divergence of bases across exchanges in futures markets.

Newer protocols, like Alkimiya and Strips Finance, aim to deepen this market, by providing mechanisms for trading floating-to-fixed swaps on staking yields and exchange-specific funding rates. This is, again in my view, a critical component of deepening liquidity and real-world usage of the cryptocurrency ecosystem.

---

In the last and final post of this series, I’ll discuss more about the parities identified here, and some speculation of what the spreads between the theoretical parities and real world prices can mean.

Cheerio.

• Lily