Note: While I have done my best to fact check this with smart folks, I cannot claim the following post is 100% accurate on all market points. It should pass the basic smell check on volatility trading and options, but please consult with your nearest textbook for more information.
I was a bit delayed writing this, due to the strangeness of my current life circumstances. In some personal news, I will be moving to the Bay Area again to pursue other things, and will be leaving my PhD program. I’m not one of those classic dropout cases where you leave because you hate it and end up on the couch or doing DoorDash for a few months while you try to figure out next steps. This came after a quarter of absence, and me realizing that despite my interest in bioinformatics, it’s undeniable that a lot of my passion has shifted over the past year to quantitative research and more math/financial topics. I’m not closing the door on academia; I fully intend to complete something, but it will likely be in mathematics and on different terms.
That said, let’s go back on topic. This is a follow-up post to my first post last month explaining the “monthly cycle” of the markets - the hedging pressures induced by options market makers and how they impact in a very regular way the markets due to the monthly options expiration cycle. This and the related concept of gamma exposure have been known both by traders and academics for a while now, but weren’t particularly notable until fairly recently with the advent of an options dominant (or degenerate) marketplace.
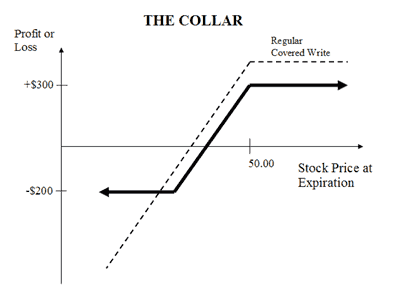
When talking about a phenomenon, it would be folly to talk about what, and leave off the who and the why. Despite popular (both on Twitter and in financial news) belief, the largest drivers of predictable option flow tends to be institutional, in the form of structured products. More specifically, in recent years, a popular structured product used by risk-averse players (e.g. retirees, pensions, etc.) has been in the form of collars — instead of holding long the underlying alone (e.g. a simple long-SPY strategy), the fund (or now, ETFs as well) can sell calls to finance put positions to cap downside volatility.
This is, due to many factors (which can be a future blog post) not necessarily a very good strategy, since it substantially caps upside. In essence, you are selling some portion of the upside (in the form of selling a call) to finance downside protection (the put).
There are several prominent variations of it, including QYLD, XYLD (selling calls only on Nasdaq and S&P 500 respectively), and the most famous, the JPM Hedged Equity Fund and its quarterly reset. In all cases (including the converse, writing puts like PUTW), this is done to reduce volatility (whether or not it does is debatable). This was discussed in great depth by Pat Hennessy on Twitter recently:

These are notable because of the massive size they represent in the market, collectively representing tens of billions of assets, and the calendrical, forced nature of how they behave. Unlike the random morass of normal market behavior, these players have well defined behaviors planed out in advance, and impact the market both by the necessary hedging (market makers have to absorb the extra calls and sell the extra puts) and front-running flows (this occurs as well when indexes rebalance, for example).
We can’t know for certain how the extra contracts impact market makers, but we can reason about it in a vacuum and make some observations.
To keep it simple, let’s imagine we’re in a universe where the only option player (other than indifferent market makers) is the JPM Fund mentioned above. Therefore, the market will be positioned solely to absorb their trades - our market makers will end up net long calls (buying them from JPM) and short puts. To keep it even more simple, let’s imagine that as a function of delta both the call and puts are equidistant at the time the collar is created. Over time, we normally expect the market to move upwards over time (thanks Jerome Powell). This means as the next expiry roles around, if the market has moved up, we expect the calls to gain delta (since the market spot price has moved closer to our strikes) and the puts to lose delta. As we’ve discussed in prior posts, this similarly occurs with gamma:
If the market moves a lot upwards, we expect that near the collar strikes the market will have high gamma exposure. This will cause our rally to “slow down” as we talked about in the previous post. However, as the market continues upwards, gamma exposure will decrease, as the collar calls move more and more in-the-money.
If the market moves a little upwards, we similarly expect that near the collar strikes the market will have high gamma exposure. The closer this occurs to the options expiration date, the more gamma this will contribute, decreasing market volatility substantially (given gamma’s relationship to time-to-expiry).
If the market moves a lot downwards, we expect that the puts bought by the collar will gain delta and therefore gamma, while the calls lose both delta and gamma. In this case, given that the market makers are short puts, this will contribute negative gamma. This will, per our prior post, lead to protracted selloff, slowing down as the puts become more and more in-the-money.
If the market moves a little downwards, we expect radically different behavior depending on how far we are from the puts sold. If the puts are still well out-of-the-money, this will decrease gamma exposure from the calls sold, but likely not bring us close to our puts (and therefore negative gamma).
In all cases, we can observe a key fact here - the impact of options positions on market behavior is a function of time (to expiry) and space (how close the spot price is to the option positions). However, a clever reader will note I left off another thing that matters here — volatility.
We talked a bit about vanna in prior posts, but the short version is vanna is a measure of how an option’s delta (or roughly, probability of ending up in-the-money at expiry) changes as a result of changes to implied volatility. Naively, we can reason that higher volatility should mean higher delta — volatility is in the most general sense a measure of how fast price is moving (this is kind of a crappy approximation, and more correctly there is market time versus wall time), and given a finite amount of time (the option expiry), the faster price moves, the more range and potential prices we can cover. This increase in potential path range means that on average, the option should be worth more than one moving slower (less volatility).
What makes this more complicated is in the real world, we do not live with constant volatility. One of the foundational assumptions of Black-Scholes, from which we derive all our Greeks, is the idea of constant volatility — volatility is fixed in relation to both time and spot price. In the real world, this does not happen. While I could wax philosophic about stuff like volatility clustering and stylized facts, the important notable difference here is what we call the spot-vol correlation.
In the real world, for better or for worse, volatility is highly tied to how price is moving. This makes sense. When we’re drifting lazily upwards (yay, summertime markets), there isn’t substantial reason to panic, and volatility tends to be low. However, if we suddenly crash 5% tomorrow, conversely, there is a lot of panic. Volatility, unlike spot price, is path dependent - if I long SPX at 4200 and it goes to 4100, then 4300, then back to 4200 and I sell, I’ve made no money. Conversely, I can reasonably expect that if the current spot price heads from 4200 to 4100 within a day, there will be a massive increase in volatility. If it heads from 4200 to 4300, usually this is accompanied by a decrease in volatility.
I’m being a bit careless with notation here, so let me clarify again this refers to implied volatility, which is assigned a single value for every given option strike/expiry (and usually is not the same for a given expiry due to volatility smiles). Implied volatility is related but differs from realized volatility, which is a measure (in context, a trailing measure) of how the market moved over a given period. To avoid yet another post topic (although I will cover it eventually in the future), implied volatility can be seen as a forecasted mirror of realized volatility lasting until the option’s expiry. Unlike the market at large, realized volatility tends to be mean-reverting with certain caveats, and a whole host of models and research exist to model how exactly volatility behaves. In the most general sense, we can all agree that there is some relationship between implied and realized volatility - in general, this takes the form of “as realized volatility trailing increases, implied volatility increases, and vice versa”.
Taking these two realizations together, we can observe three things about equities:
1) In our short put/long call example, as the market moves higher consistently (e.g. as we observed from late March to mid April 2021), volatility should decline. This will cause the delta of our short calls and long puts to both decrease, all other factors remaining equal.
2) Vanna behaves similarly to gamma in some ways, and very different in other ways. Similar to gamma, vanna tends to concentrate as time-to-expiry gets closer at the ATM strikes. However, unlike gamma it tends to diminish rapidly close to expiry as well (volatility tends to zero), and takes a more tilde-shape (~) as a function of spot price, versus the witch’s hat shape of gamma.
3) As time-to-expiry ticks down, gamma increases at-the-money and decreases out-of-the-money.
Putting these together, and we can make some interesting observations about the monthly OPEX. Let’s zoom out a bit from our JPM-only options world, and take two assumptions prima facie:
1) The at-the-money strike in general tends, for all times-to-expiry (tenors), to be the most liquid and have the highest volume compared to more OTM strikes. This isn’t exactly correct and does not hold always, but holds well enough in practice on many instruments (especially the SPX complex).
2) The options market tends to evolve similarly over time to the underlying equity market. This is implied to some degree by #1 — we expect that as the spot price of the underlying moves over time, so will the strike prices traded in the equity’s options market.
What this means, dollars and cents, is that options positioning and its impact on the underlying markets, is largely path dependent. Taking it on a monthly cycle, I tend to use a few rule of thumbs derived from the above assumptions:
Gamma exposure tends to end up higher when the market ends up where it spent a lot of time this month - This is a very, very rough assumption, based on assuming relatively constant volume/deltas for options purchased over time. Intuitively, if the market stays in place for a while, more open interest will naturally accumulate in range. As time-to-expiry ticks down (the aforementioned MOPEX week), this means a larger portion of open interest will remain near or at-the-money, which means gamma exposure will be higher.
The evolution of gamma exposure as time ticks down is related to the distribution of the open interest - This is a lot of fancy words to explain a fairly simple concept. As time-to-expiry draws near, due to charm, the delta of out-of-the-money options (and hence its derivatives, like vanna and gamma) decreases. The more of our open interest sits close to the current spot price (again, holding other factors constant), the more gamma should remain ‘longer’, up to the point of expiry. This leads to increased pinning action. Conversely, the more distributed open interest is, the quicker large chunks of the open interest become “dead” delta, and the quicker gamma exposure falls.
As time-to-expiry ticks down, the impact of vanna becomes substantially more precarious - I’ve referred to this as the “pin slip” colloquially. As discussed in the prior point, depending on how dispersive open interest is, as we get really close to expiry gamma exposure changes rapidly. In the days (or sometimes hours) before expiry, large chunks of the monthly chain open interest is “dead” delta/gamma, and the pinning effects of gamma exposure diminish rapidly. This is vanna’s show time. A sudden jolt downwards (or even upwards, in some cases), will reanimate our dead delta, and due to the action of both vanna and gamma, this can be fairly dramatic (especially on the downside, due to the aforementioned short put assumption). On the downside, this is compounded in regimes where market makers are short puts (and hence short gamma), leading to the behavior described in the first post. This can lead to fairly dramatic selloffs in OPEX week when the pin breaks, as observed in March and June OPEX periods on SPX.
One thing to note about these effects is unfortunately, they do tend to be statistical. Due to the inherent nature of dynamic systems like the whole market as well as the operating space of these large ETFs (aka S&P 500, the most liquid equity complex on Earth), it’s very difficult to suss out these effects to a predictive level (although many come close!). Additionally, it is very much regime-dependent: in many of the above examples, we made tacit assumptions (that market makers for example are short puts, long calls, and hedge in the underlying always). These do not always hold, and one has to be aware of when they hold better or worse.
To close this post out, I’m reminded of my initial analogy to describe this weird system, especially for the non-mathy among us. Let’s talk about The Umbrella (not the Academy, at least this time).
We can imagine that all the potential option strikes for a given equity instead of being a number line make up an umbrella, radiating out from the center (which is always the current underlying’s spot price). This umbrella represents the maximum amount of open interest for a given monthly option chain.
In general, people are lazy, and as the month ticks on, most times people will pick options near the center of the umbrella. But remember, the center moves over time (spot price moves). So over time, open interest that was at the center becomes no longer at the center (sometimes it moves off the umbrella entirely if far enough).
We can imagine the market, or rather the current underlying market, is sitting comfortably underneath the umbrella. When the umbrella is large and filled in (lots of gamma exposure), the options umbrella protects us from volatility (via gamma exposure). The market stays calm and pinned.
However, this is temporary, like most things are. As the month ticks down, the umbrella starts to close. At first, this closing is slow. Later, it quickens, dramatically. In the final hours, it snaps shut.
If a ton of the center of the umbrella is filled in (aka the open interest is mostly clustered around the current spot price), even as the sides of the umbrella close in, the market is still protected from volatility for longer. However if the umbrella is diffuse, or if it is filled in on the sides and empty in the center, our gamma umbrella gives way much quicker.
In the final stretch (the week before MOPEX, more or less), strange things happen, largely due to this non-linear relationship.
At-the-money gamma increases, and our umbrella strengthens in the center. The market stays pinned. There’s some interesting effects related to pre-weekend hedging in the final stretches, but I’ll leave those to more experienced options market makers to explain.
However, this is a temporary effect. The umbrella is still closing, no matter how much we strengthen the center due to tasty ATM gamma. There always is a point - whether a day, half a week, or an hour - pre expiration where most of our ATM gamma exposure has now fallen away (the umbrella has closed far enough). This is when vanna and OTM gamma can kick in. Any perturbation, moving us from our pinned position to (usually a lower) another position, causes the umbrella to snap back open. Given the usual assumption (on SPX) of short puts/long calls, this tends to lead to a situation whee market makers are short gamma, exacerbating the severity of a selloff.
—
With this, I conclude the long-due MOPEX series. I hope you enjoyed it!
Lily Francus




mine too