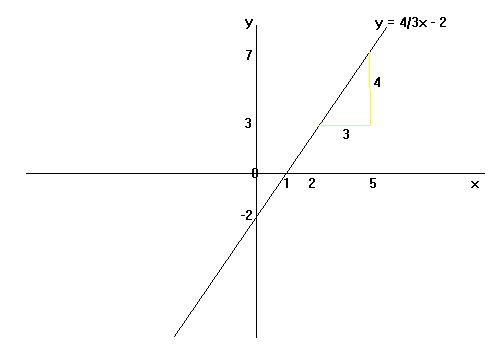One of the most interesting observations of options flows is the pretty stable (especially recently) relationship between the time of the month and index (specifically SPX and its compliments like SPY, VOO, etc.) returns.
This knowledge is getting more prevalent (which is a good thing), and in this post I will dissect the probable mechanisms for this options-related cycle.
It’s unclear to me if this was a predominant effect before last year, or appeared largely due to options dominance. However, a recent tweet shows the outsized impact on returns since at least late 2020:
In my prior post on, we simply derived the first-order Greeks (vega, rho, delta, theta) from the quantities allowed to vary in the Black-Scholes equation. It ends up being fairly intuitive. However, unlike a simple differential function (e.g. y = x) where you can take the derivative a finite number of times (dy/dx = 1 in that example, and you cannot meaningfully derive higher order derivatives), the quantities that the Black-Scholes price depends on are more or less infinitely differentiable, or what mathematicians call smooth. What does that mean exactly?
If we go back to the (mostly correct, at least in Euclidean spaces) analogy of derivatives being akin to the slope of a straight line (although more curvy I suppose), we can see that the first derivative here is the slope (4/3).
In functions like the parabola (y = x^2), we can take the first derivative to get the “slope” at any given point, which is 2x. What this means is that if x = 4, we expect the “slope” at that point to be 8 (2 x 4).
What’s interesting though is we can also find the “slope” of the “slope” — how fast is the slope changing? This is the second derivative—we can see in our first derivative y = 2x that x is still present. Hence it is differentiable again — the second derivative being 2. This means that for every one unit of x changed (let’s say 4 to 5) we expect the slope at that point to change by 2 (the slope of the slope).
Ignoring the basic Calculus review, how is this useful for us with Black-Scholes?
The nifty thing is the quantities in the equation depend on each other.
Let’s go back to the equation:
As we mentioned in the prior post, if we take C(s, t) to be y, we have four quantities which can be our “x” (it’s a partial differential equation, so you pretend all the others are constants except the one you’re modeling):
The strike price of the option (this is always fixed/constant for a single vanilla option)
The current stock price (the spot)
The risk free interest rate
Volatility
Time left to maturity
What’s interesting to note however, is that several factors here depend on each other. For example, we derived delta as the change of our “y” (the call option price) as the spot price changes (the “x”).
I’m not going to delve too much into the weeds here, but delta can also be interpreted (to rough approximation) as the probability that for the given option, it expires in-the-money (by any amount). This doesn’t hold exactly in practice, but helps us understand the delta of an out-of-the-money option.
At expiration, the option contract can take only one of two states:
In-the-money: This pays you out the intrinsic value, which is the current stock price - the strike price (for a call, the strike price - current stock price for a put).
Out-of-the-money: This is worthless.
What this means is that at expiry, delta will always be either 0 or 100 (no in-between). However, you cannot in practice hedge that because it is a massive discontinuity. If I were to sell you an option for $3 and now it’s worth either $10 or $0, I will potentially make a pretty substantial loss. Delta helps us smooth this discontinuity—for an out of the money option, it has value pre-expiration due to the option’s “optionality”—the extrinsic (time) value, the chance that the option will expire in the money.
That said, this isn’t linear (again, will avoid the specifics). If we imagine an option strike price at $50 with a week left on the contract, it’s significantly more likely that it will be at or above $50 if the underlying’s current price is $45 and not $40. This is why delta (and other Greeks) demonstrate convexity—unlike our slope example (a straight line), they act more like parabolas with respect to various things (price, time, volatility, etc.).
This convexity gives us what nerds call the higher-order Greeks—the slope (and slope of slope, etc.) of the various first-order Greeks with respect to each other.
Some examples (not exhaustive, but the important ones):
Gamma
Gamma is perhaps the most interesting one to most people, because it causes neat things to happen like shit companies exploding in value due to buying call options (although arguably, it’s not just gamma but vanna too).
Gamma is simply how delta changes with respect to the current underlying price. Or, if we unpack what delta is (the change in option price with respect to the current underlying) gamma could be interpreted as “the increase/decrease in how much the option price is changing as the underlying stock moves up or down”.
This is intuitive for the most part—as mentioned before, if we imagine an option strike price at $50 with a week left on the contract, it’s significantly more likely that it will be at or above $50 if the underlying’s current price is $45 and not $40.
Because of this, we expect that the closer we get to the option going in the money (and having a real value at expiration), the faster its delta should grow (the chance it expires in the money). There’s some really nice and boring statistical proofs of this fact, or you could just take my word for it. This holds even as you hold the option — if you are long a call option in the above example, you should see it increase more in value from $45 to $46 than from $40 to $41.
This holds on both sides of the spectrum (in and out of the money)—an option as it gets deep in the money no matter how much time remains starts to lose all of its gamma goodness, since the maximum delta you can have is 100 (and minimum is 0). So the more you move away from the at-the-money point (the strike price), the less gamma you’re gonna have.
This behavior gets really important when you start factoring in time into the equation, which I’ll talk about in my next post.
Vanna
One of the haute new Greeks to be talked about on the scene, vanna measures how delta changes with respect to the volatility.
Vanna is hard especially for newer traders to grasp, because unlike gamma it’s fairly unintuitive. Why does the delta of an option change based on volatility?
Let’s consider it from the perspective of someone trying to “hedge” the option (as we explained in the first post).
The extrinsic (time) value of an option represents the “possibilities” that may happen during the lifetime of an option. I’m going to avoid getting into volatility-time since that’s too complicated here, but essentially the Black-Scholes factors in volatility in order to price where, at the expiry of the option, the stock price can be (not will be).
A stock that moves dramatically (like Tesla) may in a week move $200 in price, while an extremely boring stock (like Altria) may budge $1 or less. Because of that, we can set up two examples:
Let’s say we have an Altria call option expiring next week. Altria is currently at $52, and the call option is for $60.
Let’s now say we have a Tesla call option expiring next week. Tesla is at $700, and the call option is for $800.
If we assume that Altria will move $1 per week and Tesla $200 per week, we can quickly see why the Tesla option should be “worth” more—there is a higher chance this week Tesla moves $100 to $800 than Altria moves $8 to reach $60.
This is why volatility matters (if you ask some people, it’s the only thing that matters). Volatility is the true tempo of what determine’s the option’s time value (not wall time!)—hence, if we go back to delta, we can immediately see why delta impacts it.
By understanding for an out-of-the-money option that delta is roughly “probability of expiring in-the-money”, we can see that with more volatility, we expect delta to go up. This is because if Altria suddenly jumps in volatility to $8 a week, our option has way more likelihood of expiring in-the-money!
Vanna is the partial derivative of delta with respect to volatility, and tends to matter a lot, especially when the market moves dramatically (in either direction). It can be naively understood to mean “the increase/decrease in how much the option price is changing as the underlying’s volatility increases or decreases”.
Charm
Unlike vanna which tends to be a bit big-brain, charm comparatively is simple to define if one understands what extrinsic value is (the option’s “option-ness”). Going back to our understanding of delta (that it will be 100 or 0 when the option expires), we can intuitively see that for an out-of-the-money option (which will expire at 0 delta) that wall time must impact its value. This tends to be much less significantly for in-the-money options, and by definition has no impact if the option is already at 100 or 0 delta.
We can also call charm delta decay, and since we agreed that all of the first-order Greeks are smooth (infinitely differentiable), we can quickly see that charm isn’t constant—an option’s charm is negligible for a far-off expiry, and extremely meaningful as the expiry draws near. This tends to accelerate quite dramatically right before expiration—the OPEX week effect I will cover in the next post.
Volga
The last of the second-orders to cover is volga, also known as vomma (sounds like vomit). Volga isn’t talked about as much, mostly because she has the shittiest name of them all (very uncreative and not even remotely Greek or science sounding).
Volga is the sensitivity of the option price’s sensitivity to volatility with respect to volatility. Or since that sounds completely incomprehensible:
Our first order Greeks, vega, measures how much the option price will change with respect to volatility changing (we can see why in our discussion on vanna).
However, this isn’t itself a straight line—a minor change in volatility doesn’t hit the same as a major change. When we quantify volatility (like in the Tesla example, arguing it moves $200/week), we can see quite easily that the value of our $800 call option should change much much more with a rapid change in volatility (let’s say to $300/week) versus a minor one ($195/week).
Volga is important especially if you manage a large book of options, and also appears in concepts like vanna-volga pricing of Forex options.
In the next post, we’re going to take all the concepts we’ve learned and discuss gamma exposure and how these second order Greeks help determine the weird monthly cycle (no, not that one) that seems to drive the market lately.